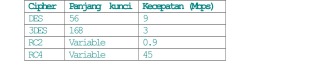
Kriptografi NOW not the Past

Kriptografi saat ini

PENDAHULUAN

1.1 Latar belakang

Perkembangan teknologi informasi dan komunikasi semakin mempermudah proses pengolahan, penyimpanan dan pendistribusian data dan informasi. Aspek kemudahan yang didapat tersebut ternyata berbanding terbalik dengan faktor confidentiality (kerahasiaan), intergrity dan availability (ketersediaan).

Proses pengiriman data yang dilakukan media seperti Local Area Network (LAN), internet, email, handphone maupun media lain; pada dasarnya melakukan pengiriman data tanpa melakukan pengamanan terhadap konten dari data yang dikirim, sehingga ketika dilakukan penyadapan pada jalur pengirimannya maka data yang disadap dapat langsung dibaca oleh penyadap. Untuk menghidari kemungkinan data yang disadap dapat langsung dibaca oleh penyadap, maka data yang dikirim diacak dengan menggunakan metode penyandian tertentu sehingga pesan yang terkandung dalam data yang dikirim tersebut menjadi lebih aman.

Salah satu metode kriptograpi yang ditawarkan untuk melakukan penyandian terhadap data adalah metode kriptografi pontifex yang menggunakan prinsip dari kartu sehingga terdapat 54! cara kartu tersebut diatur.

1. 1. Tujuan

Tujuan penulisan untuk mengetahui prinsip dasar dari proses penyandian dengan menggunakan algoritma kriptografi Pontifex.

TINJAUAN PUSTAKA

2.1 Terminologi

Kriptograpi (cryptography) adalah studi mengenai metode penyandian pesan yang bertujuan untuk menghindari perolehan pesan secara tidak sah^[3]. Kriptografi (cryptography) merupakan ilmu dan seni untuk menjaga pesan agar aman. (Cryptography is the art and science of keeping messages secure) ^[1]. “Crypto” berarti “secret” (rahasia) dan “graphy” berarti “writing” (tulisan)^[5]. Para pelaku atau praktisi kriptografi disebut cryptographers. Sebuah algoritma kriptografik (cryptographic algorithm), disebut cipher, merupakan persamaan matematik yang digunakan untuk proses enkripsi dan dekripsi. Biasanya kedua persamaan matematik (untuk enkripsi dan dekripsi) tersebut memiliki hubungan matematis yang erat.

Proses yang dilakukan untuk mengamankan sebuah pesan (yang disebut plaintext) menjadi pesan yang tersembunyi (disebut ciphertext) adalah enkripsi (encryption). Ciphertext adalah pesan yang sudah tidak dapat dibaca dengan mudah. Menurut ISO 7498-2, terminologi yang lebih tepat digunakan adalah “encipher”. Proses sebaliknya, untuk mengubah ciphertext menjadi plaintext, disebut dekripsi (decryption). Menurut ISO 7498-2, terminologi yang lebih tepat untuk proses ini adalah “decipher”.

Cryptanalysis adalah seni dan ilmu untuk memecahkan ciphertext tanpa bantuan kunci. Cryptanalyst adalah pelaku atau praktisi yang menjalankan cryptanalysis. Cryptology merupakan gabungan dari cryptography dan cryptanalysis. Kriptograpi merupakan bidang pengetahuan yang cukup tua. Kriptograpi digunakan oleh Julius Caesar dalam perang Gallic, walaupun saat itu hanya menggunakan metode sederhana dengan melakukan pergeseran pada urutan huruf. Secara garis besar proses kriptograpi terdapat dua bagian yaitu enkripsi dan dekripsi.

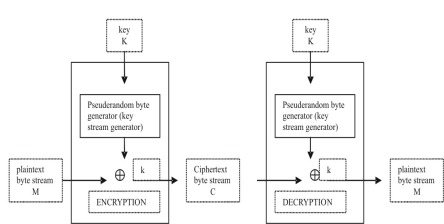
Gambar di bawah ini mengilustrasikan bagian proses kriptograpi

Gambar 2.1 Sistem Kriptograpi

2.2 Algoritma Berdasarkan Key ^[3]

Terdapat dua macam algoritma kriptograpi yaitu algoritma Public Key (Asymetric) dan Secret Key ( Simetric). Algoritma simetrik sendiri terdiri atas block chipper dan stream chipper. Gambar di bawah mempersentasikan jenis kriptograpi berdasarkan key yang

Dipakai.

Gambar 2.2 Pembagian Algoritma Kriptograpi Berdasarkan Key

2.2.1 Algoritma Asimetrik

Public Key menggunakan dua key yang berbeda dalam melakukan proses enkripsi dan dekripsi. Public Key yang digunakan untuk melakukan enkripsi dan boleh diketahui umum. Sedangkan Private Key hanya boleh diketahui oleh pihak penerima.

2.2.2 Algoritma Simetrik

Key yang digunakan pada algoritma ini, antara pengirim dan penerima adalah sama, sedangkan proses yang dilakukan untuk dekripsinya melakukan kebalikan dari proses enkripsi. Kekuatan algoritma simetrik sangat bergantung pada satu key yang digunakan. Jika key dapat dikirimkan secara aman maka kemungkinan mendapatkan plaintext dan chipertext yang dikirimkan akan semakin kecil. Algoritma Simetrik memiliki dua tipe dasar yaitu Block Chiper dan Stream Chiper. Dengan menggunakan block chiper , plaintext chiper yang sama dengan key yang sama akan dienkripsikan ke dalam Chipertext Block yang sama. Pada Stream Chiper , Plaintext atau byte yang sama akan dienkripsikan ke dalam bit yang berbeda setiap enkripsinya^[3].

1 Stream Cipher

Stream Chiper melakukan pengkodean 1 bit atau byte dalam satu kali prosesnya Stream Chiper lebih muda diimplementasikan dalam hardware. Hardware bekerja berdasarkan bit-bit yang merupakan satuan terkecilnya dalam melakukan proses perhitungannya.

2 Block Chiper

Block Chiper melakukan pengkodean 1 block dalam sekali proses. Ukuran block ini sendiri dapat ditentukan sesuai keinginan. Namun dalam prakteknya ukuran block yang digunakan memenuhi rumu 2ⁿ dengan n bilangan integer.

3 Perbedaan Stream Cipher dan Block Cipher

Stream Cipher dan Block Cipher sebenarnya memiliki karakteristik yang sama. Stream Cipher dapat diimplementasikan sebagai Block Cipher dan sebaliknya. Perbedaan Stream Cipher dan Block Cipher didefinisikan.

“Block Cipher melakukan prosesnya pada data dengan transformasi yang tentu pada suatu ukuran besar blok data dari Plaintext, Stream Cipher bekerja berdasarkan pengolahan digit Plaintext tersendiri dengan transformasi yang berbeda-beda setiap waktunya”.

2.3 Kriteria Algoritma Kriptograpi^[3]

Kriteria standar yang harus dimiliki oleh suatu algoritma kriptograpi menurut National Bureau Of Standarts (NBS), sekarang dinamakan National Institute of Standarts and Tehcnology (NIST), adalah

• Algoritma harus memiliki tingkat keamanan yang tinggi

• Algoritma harus spesifik dan mudah dimengerti

• Tingkat keamanan algoritma harus terletak pada key, bukan dari kerahasiaan algoritmanya

• Algoritma harus dapat diadaptasi pada aplikasi yang beragam

• Algoritma harus ekonomis dalam pengimplementasiannya pada perangkat keras.

• Algoritma harus efisien dalam penggunaannya

• Algoritma harus dapat berlaku secara umum

• Algoritma dapat dipisahkan (tidak bergantung)

2.4 Dasar Matematika

Banyak teori yang menjadi dasar pembangunan algoritma kriptograpi. Dalam tugas akhir ini akan ditampilkan beberapa teori saja yan berhubungan dengan algoritma Pontifex dalam implementasi dan analisisnya.

2.4.1. Teori Informasi

Mendefenisikan jumlah bit terkecil yang diperlukan untuk mempersentasikan informasi. Jika terdapat 7 kemungkinan maka jumlah bit yang diperlukan adalah 3 diperoleh dari pengambilan nilai terkecil yang masih dapat menampang 7 representasi data yaitu 2³ = 8

2.4.2 Kompleksitas Algoritma

Ditentukan dengan kekuatan perhitungan yang diperlukan untuk mengeksekusinya. Perhitungan kompleksitas ditentukan berdasarkan dua variable T (Time) waktu dan S (Space) ruang memory yang dibutuhkan. Jika waktu yang diperlukan untuk melakukan proses selalu tetap maka kompleksitasnya dikatakan konstan. Bila waktu berbanding lurus dengan proses dikatakan linear.

2.4.3 Teori Bilangan

Teori bilangan banyak digunakan dalam teknik kriptograpi, teori bilangan yang berhubungan dengan tugas akhir ini, diantaranya :

Modulo (Mod)

Modulo bekerja berdasarkan pada rumus b = c – (a * n)

Dengan a bilangan yang memodulo, b hasil modulo, c bilangan yang dimodulo dan n merupakan nilai integer. Hasil modulo harus terletak antara 0 hingga n – 1.

Prima (Prime)

Bilangan prima adalah nilai yang hanya memiliki dua factor dirinya sendiri dan 1, a dikatakan bilangan prima jika faktornya hanya a dan 1.

Generator dan Primitive

Jika p adalah bilangan prima dan g kurang dari p maka g adalah generator mod p jika

For each b from 1 to p-1, there exist a where g’ = b (mod b)

Dengan kata lain g primitive terhadap p

Inverse Modulo Number ( modulo balikan)

Penulisan inverse bermakna balikan. Jika dalam modulo uang diinginkan adalah harga b, maka dalam inverse modulo yang dicari adalah c. dengan notasi matematika c =(a * n) +b

Dimana a, b, c dan n sesuai dengan ketentuan pada modulo

Greatest Common Divisor

Dua bilangan dikatakan relative prima jika irisan factor pembagi kedua bilangan hanya 1

Dengan notasi matematika

Gcd(a, n) = 1

Generator

Jika pa adalah prima dan g kurang dari p maka g adalah generator mod p bila

For each b from 1 to p -1, there exist a where g^a = b (mod p)

Jacobi Symbol (Simbol Jacobi)

Notasi J(a-n) merupakan bentuk umum dari symbol langrange dari beragam modulo, didefinisikan untuk sembarang bilangan integer a dan bilangan ganjil n.

Metode Jacobi memiliki ketentuan

1. J(a,n) hanya didefinisikan untuk nilai n ganjil

2. J(0,n) = 0

3. Jika n bilangan prima maka J(a,n) = 0 bila n membagi a

4. Jika n bilangan prima maka J(a,n) = -1 bila a adalah residu quadratic modulo n

5. Jika n bilangan prima maka J(a,n)=-1 bila a adalah non residu modulo n

6. Jika n adalah composite (campuran) maka

J(a,n) = J(a,p1)*…*J(a,p_m) factor prima dari n

Aturan Jacobi

1. J(1,n)=1

2. J(a*b,c)=J(a,n)*J(b,n)

3. J(2,n)=1 jika (n² -1)/8 adalah genap, selain itu J(2,n)=-1

4. J(a,n) = J(a,mod n),n)

5. J(a,b₁*b₂) = J(a,b₁)*J(a,b₂)

6. Jika Ged(a,b)=1 dan a,b keduanya bilangan genap

6.a. J(a,b) = J(b,a) jika (a-1) (b-1)/4 adalah bilangan genap

6.b. J(a,b) = -(b,a) jika (a-1) (b-1)/4 adalah bilangan ganjil

Prime Number Generator (generator bilangan prima)

Bilangan prima berperan cukup banyak dalam teknik kriptograpi. Cara yang digunakan untuk mengenerate bilangan prima adalah dengan melakukan

1. Generate bilangan random

2. Periksa apakah bilangan tersebut prima

3. Masukan bilangan tersebut ke dalam kumpulan bilangan prima

Terdapat beberapa cara yang dapat diterapkan untuk membangun bilangan prima, metode dibawah ini memeriksa apakah p bilangan prima.

Solovary Strassen

1. pilih nilai random, a, kurang dari p

2. jika ged(a,p) 1 maka p bukan prima

3. lakukan perhitungan J=a^(p-1)/2 mod p

4. lakukan perhitungan Jacobi J(a,p)

5. jika jJ(a,p) maka p mutlak bukan prima

6. jika j = J(a,p) maka kemungkinan p bukan prima < 50 %

Lehmann

1. Pilih nilai random,a kurang dari p

2. Lakukan perhitungan Jacobi J=a^(p-1)/2 mod p

3. Jika J=a^(p-1)/2 mod p 1=1 atau -1 (mod p) , maka p mutlak bukan prima

4. jika a^(p-1)/2=1 atau -1 (mod p), maka kemungkinan p bukan prima < 50%

Rabin Miller

Pilih nilai p sebarang, lakukan perhitungan b dengan nilai b adalah nilai jumlah perkalian 2 dibagi (p-1) kemudian hitung nilai m dengan rumus p = 1 + 2 b* m

1. pilih nilai random, a kurang dari p

2. set j = 0 set z = a^m mod p

3. jika = – 1 atau jika z = p -1 maka p valid akan kemungkinan prima

4. jika j > 0 dan z = 1 maka p bukan prima

5. set j = j + 1, jika j < b dan z p -1, set z = z² mod p dan lakukan proses 4 jika z = p-1, maka p valid kemungkinan prima

6. jika j=b dan z p-1 maka p bukan prima

Metode Praktis

1. Generated n-bit bilangan random p

2. set bit high order dan low order bit menjadi 1

3. periksa p, dapatkah dibagi oleh bilangan prima kurang dari nilainya. Kebanyakan implementasi hanya menggunakan bilangan prima kurang dari 256. efisiensi dari pemeriksaan bilangan prima dilakukan dengan membagi bilangan tersebut dengan bilangan prima < 2000

4. lakukan proses Rabbin Miller untuk nilai random a. jika p sesuai maka generator bilangan random a lainnya dan ulangi lagi test. Pilihlah nilai a yang kecil untuk mempercepat proses perhitungan. Proses ini dilakukan 5 kali.

2.5 Manajemen Key

Pengaturan key pada metode simetrik mutlak diperlukan, terdapat beberapa hal yang menjadi acuan dalam melakukan pengaturan key.

2.5.1 Generate Key

Kerahasiaan key sangat bergantung pada cara key itu di generate. Generate key yang paling baik adalah key yang sedekat mungkin random. Nilai yang benar-benar random sulit didapat jika mesin yang membuat nilai random tersebut memiliki nilai tertentu. Pseudo random Generator merupakan generator bilangan random yang cukup baik. Namun tetap saja memiliki nilai tidak random.

2.5.2. Lama Penggunaan Key

Semakin lama key dipakai atau disimpan maka akan semakin rendah keamanan data yang dienkripsi. Hal terbaik adalah menggunakan key sekali pakai dan tidak menyimpan key pada media penyimpan permanen (misalnya harddisk). Lakukan pergantian key dalam kurun waktu yang tertentu yang optimal. Jika ingin menghilangkan/mengganti key maka lakukan dengan seaman mungkin. Wipe area yang dijadikan tempat penyimpanan key.

2.6. Pertukaran Key

Pertukaran key merupakan titik yang paling rawan diserang untuk memecahkan algoritma kriptograpi. Terlebih lagi pada algoritma simetik yang sangat mengandalkan pada kerahasian key-nya.

Metode yang digunakan dalam pertukaran key adalah

2.6.1. Enrypted Key

Metode ini melakukan enkripsi terlebih dahulu sebelum key yang sebenarnya dikirim. Pada kedua sisi pengirim dan penerima harus memiliki key Encypted key yang sama dalam melakukan enkripsi. Kelemahan metode ini terdapat pada key Encypted Key yang digunakan jika seseorang mengetahui Key Encypted Key-nya maka enkripsi sebelum key dikirimkan adalah percuma dan hanya memperlama proses tanpa meningkatkan keamanannya. Segala serangan pada metode ini terfokus pada key encypted key yang digunakan.

2.6.2. Diffie Hellman

Metode yang cukup cerdik ditemukan oleh Diffie Hellman. Keamanan metode ini berasal dari permasalahan perhitungan algoritma diskrit, dibandingkan dengan melakukan perhitungan exponensial pada domain yang sama.

Aturan matematika yang pakai dalam metode ini cukup sederhana. Pertama-tama, tentukan bilangan prima n dan g dimana g adalah primitive mod n. nilai prima m tidak perlu rahasia . kedua nilai ini haruslah sama pada pengirim dan penerima.

Algoritma pertukaran Key-nya adalah

Dengan kesepakatan

A = Pengirim pertama

B = Penerima pertama

1. A memilih nilai integer x yang cukup besar dan mengirim

X = g^x mod n.

2. B memilih nilai random y yang cukup besar dan mengirim

Y = g^y mod n

3. A melakukan perhitungan

K = Y^x mod n

4. B melakukan perhitungan

K’ = X^y mod n

Keduanyan nilai k dan k’ adalah sama dan bersesuaian dengan nilai g^xy mod n . seorang yang dapat melakukan penyadapan informasi yang dikirim hanya akan mengetahui nilai n, g, X dan Y tetapi tidak mengetahui nilai k dan k’, kecuali penyadap dapat menghitung nilai logaritma diskrit.

Pemilihan k dan g sangat berpengaruh pada tingkat keamanan. Nilai (n-1)/2 haruslah bilangan prima dan nilai n merupakan bilangan yang cukup besar.

2.6.3. Extended Diffie Hellman

Kelemahan yang dimiliki metode Diffie Hellman adalah kita tidak dapat menentukan key yang akan ditransmisikan, diperlukannya konfirmasi dari penerima untuk membentuk sebuah key. Permasalahan ini diatasi oleh metode Extended Diffie Hellman. Dengan ketentuan seperti Diffie Hellman, algoritma pertukaran key-nya adalah

1. A memilih nilai integer x yang cukup besar dan mengirim

K = g^x mod n.

1. B memilih nilai random y yang cukup besar dan mengirim

Y = g^y mod n

1. A melakukan perhitungan

X = Y^x mod n

1. B melakukan perhitungan

= y^-1

K’ = X^x mod n

Algoritma ini akan menghasilkan k dan k’ yang bernilai sama

2.7 Penanganan Error

Penanganan error yang paling buruk dari sisi biaya adalah dengan melakukan pengiriman ulang data yang telah dikirimkan. Namun metode ini sangat baik untuk menjamin data yang diterima tidak terdapat error. Kelemahan metode ini selain dari sisi biaya adalah jika saat data dikirimkan ulang oleh penerima dan data mengalami kerusakan dalam pengiriman ulang maka data akan dikirim ulang oleh pengirim pertama. Tentunya hal ini merupakan pemborosan.

2.8 Metode Parity Check

Metode ini didasarkan pada pemberian bit parity pada data, data yang dikirimkan dilakukan pemeriksaan genap atau ganjil. Parity diberikan sebagai penandanya. Kelemahan metode ini jika terdapat error bit dalam bilangan genap maka parity cek tetap akan benar padahal data yang dikirimkan tidak sesuai. Namun demikian metode ini sangat murah dalam implementasinya dan cocok untuk jaringan dengan error rate yang rendah. Metode ini merupakan layanan pada Datalink layer tetapi dapat diadaptasi ke dalam Applicatation Layer

ALGORITMA KRIPTOGRAPI PONTIFEX

3.1 Pengenalan Algoritma Pontifex

Pengenalan Algoritma Pontifex merupakan Algoritma Stream Chiper OFB (Output FeedBack). Algoritma mendapat keamanan dari permasalahan kartu. Dalam pembuatan key-nya, algoritma ini mengandalkan decking dari 54 kartu. Dengan demikian terdapat 54! Cara kartu tersebut diatur. Algoritma ini tidak seperti algoritma Stream Chiper pada umumnya yang memiliki S-box dan P-box serta key yang dibarengi sub-key. Pontifex memiliki nama lain solitare dan diciptakan oleh Bruce Schneier. Bruce Schneier juga menciptakan algoritma kriptograpi lainnya, dalam Block Chiper yang dinamakan Two Fish. Karena perbedaan dalam perancangannya maka tidak semua bagian dari algoritma ini dapat dibandingkan dengan algoritma Stream Cipher lainnya. Namun faktor dasar dari kriptograpi selalu dapat dibandingkan dengan semua metode. Faktor tersebut adalah waktu, tingkat keamanan dan biaya. Penganalogian dengan kartu, dalam implementasinya akan dikonversi kedalam nilai bilangan.

3.2 Komponen Algoritma Pontifex

3.2.1 Komponen Dasar Pontifex

Dengan memanfaatkan 54! Macam decking kartu, maka terdapat sekitar 2,3 * 10 ⁷¹ kemungkinan kartu di – deck. Selain mendapatkan kunci dari decking kartu algoritma ini juga dapat memanfaatkan kunci yang dimasukkan dari pengguna walaupun akan sangat membebani pada kenyataannya. Secara garis besar komponen pembentuk algoritma pontifex adalah

1. Aturan Decking

• • Aturan Decking Pontifex

  • Masukan dari user

1. Otak Pontifex

2. Aturan pengambilan Key

3. Penggabungan dan pemisahan antara plaintext dan chiphertext

3.2.2 Komponen Pendukung

Tanpa komponen pendukung yang cukup pontifex bukanlah algoritma yang baik, seperti kebanyakan metode simetris yang mengandalkan pada key maka segala kekuatan pontifex hanyalah pada key. Karenanya harus ada komponen pendukung dalam pertukaran key. Selain faktor tersebut terdapat faktor lain yang mempengaruhi performansi algoritma ini. Komponen berikut adalah komponen yang digunakan sebagai optimasi algoritma pontifex, yaitu :

1. Pertukaran Key

• • Pertukaran biasa

  • Diffie Hellman

  • Extended Diffie Hellman

1. Aturan pertukaran data dalam TCP/IP

Karena pengimplementasiannya menggunakan protocol TCP/IP dengan layanan windows socket.

3.3. Proses Algoritma Pontifex

Aturan Key Generator merupakan pembeda pontifex dengan algoritma lainnya. Aturan generate kunci pada pontifex adalah

1. Fase persiapan

Lakukan pengacakan kartu menggunakan Pseudo Random Generator

1. Fase Inti

• Tentukan Joker A dalam hal ini nilai 53, pindahkan ke belakang 1 kartu dibelakang lokasi sekarang jika kartu paling belakang, maka letakkan ke belakang kartu terdepan

• Temukan Joker B dalam hal ini nilai 54, pindahkan ke belakang 2 kartu jika kartu paling belakang maka letakkan ke belakang kartu kedua terdepan. Jika kartu terletak satu kartu sebelum belakang maka letakkan kartu dibelakang kartu terdepan.

• Lakukan Triple Cut

• Dilakukan dengan cara memindahkan kartu yang terdapat pada bagian kiri joker pertama dan kartu yang terletak pada bagian kanan joker kedua. Jika joker keduanya berada pada ujung maka tidak perlu melakukan operasi ini.

• Lakukan Count Cut

• Periksa kartu terakhir, pindahkan mulai dari karti 1 hingga kartu ke (nilai kartu terakhir). Letakkan disamping nilai kartu terakhir dengan urutan yang sama.

1. Fase Pengambilan Kunci

• • • Temukan kartu yang dijadikan kunci

Berdasarkan metode pengambilan kunci dari deck. Default-nya adalah dengan mengambil kartu di kanan kartu pertama dengan jarak nilai kartu pertama tersebut. Dapat dimodifokasi dengan memasukkan kunci dari pemakai.

Ketiga fase ini dilakukan sebanyak stream karakter yang diterima dengan deck pada fase persiapan merupakan keluaran dari fase sebelumnya.

3.3.1. Fase Persiapan

Fase ini merupakan tahap pengacakan kartu yang bertujuan menentukan nilai deck awal yang akan digunakan dalam melakukan Generate Key. Deck yang dihasilkan haruslah memiliki kesepakatan antara pengirim dan penerima. Cara yang dilakukan dalam melakukan decking adalah

• Nilai kartu diurutkan dari 1 hingga 54 kemudian diberikan kesepakatan dalam peletakan joker A dan joker B.

• Melakukan randomisasi kartu dengan menggunakan Pseudo Random Generator

3.3.2. Fase Inti

Pada bagian ini akan dijelaskan secara mendetail proses yang dilakukan dalam algoritma Pontifex. Untuk memudahkan penjelasan maka akan diberikan kasus secara langsung yang berhubungan dengan aturan umum maupun khusus pada algoritma ini.

Misalkan kartu yang dideck adalah kartu terurut, setelah dikonversi menjadi nilai

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54 (……0)

Selanjutnya dalam pembahasan algoritma pontifex akan merujuk kepada nilai bilangannya, bukan nama kartunya (hanya untuk memudahkan)

1. Temukan Joker A, kartu yang bernilai 53

Posisi kartu sebelum dilakukan proses 1

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54 (……0)

Kartu ditemukan dengan posisi 53, kemudian dilakukan perpindahan kartu ke bawah contoh ini dipindahkan ke sebelah kanan

Nilai kartu setelah dilakukan proses 1 adalah

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,54,53 (……1)

1. Temukan Joker B, kartu yang bernilai 54

Posisi kartu sebelum dilakukan proses 2

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,54,53 (……1)

Kartu ditemukan dengan posisi 53, kemudian dilakukan perpindahan kartu ke bawah 2 tempat dari posisi awal pada contoh ini pindahkan kesebelah kanan 2 posisi.

Nilai kartu setelah dilakukan proses 1 adalah

1,54,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,(…2)

Pada kondisi di atas letak kartu tidak lagi paling bawah tetapi pada posisi di bawah kartu pertama. Kondisi ini merupakan kasus khusus, logikanya menggunakan perputaran dengan menganggap kartu lanjutan setelah kartu terakhir adalah kartu teratas.

1. Lakukan Triple Cut

Aturan dalam melakukan Triple Cut adalah dengan menukar kartu sebelah kiri joker terdepan ke sebelah kanan kartu joker kedua.

Untuk lebih jelasnya akan diberikan contoh kasus yang berbeda penanganannya

Kasus 3.1 Kasus Umum

Kartu sebelum dilakukan proses 3

1,2,3,4,5,6,7,8,9,10,11,12,54,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,53,42,43,44,45,46,47,48,49,50,51,52

Kartu setelah dilakukan proses 3

42,43,44,45,46,47,48,49,50,51,52,54,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,53, 1,2,3,4,5,6,7,8,9,10,11,12

Kasus 3.2 salah satu kartu joker terletak di ujung (sebelah kiri atau kanan)

Kartu sebelum dilakukan proses 3

1,54,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,(…2)

Kartu setelah dilakukan proses 3

54,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,1(…3)

Kasus 3.3 kedua kartu joker terletak di ujung

Kartu sebelum dilakukan proses 3

54,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53

Kartu setelah dilakukan 3

54,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53

terlihat pada kasus 3.3 tidak ada perubahan kartu karena tidak terdapat kartu disebelah kiri joker terdepan maupun kartu disebelah kanan joker kedua.

1. Lakukan Count Cut

Pada proses ini dilakukan optimasi terdapat dua cara yang digunakan

Cara 1 Menggunakan proses standar dari Pontifex

Periksa kartu terakhir, pindahkan mulai dari kartu 1 hingga kartu ke (nilai kartu terakhir). Letakkan disamping nilai kartu terakhir dengan urutan yang sama

Cara 2 Menggunakan Key dari pengguna

Jika perpindahan kartu pada proses Pontifex berdasarkan kartu terakhir maka pada cara kedua dilakukan dengan melihat nilai key yang dimasukan pengguna. Misalkan pengguna memasukkan key “FOO” maka pada perulangan pertama menggunakan karakter F yang bernilai 6. jadi melakukan perpindahan 6 kartu terdepan ke dekat kartu terakhir.

Menggunakan cara 1. aturan standar dari Pontifex

Kasus 4.1 kartu terakhir adalah kartu bernilai 53 atau 54

Kartu sebelum dilakukan proses 4

54,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,1(…3)

Kartu setelah dilakukan proses 4

2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,1(…4)

Kasus 4.2 kartu terakhir adalah kartu bernilai 53 atau 54

Kartu sebelum dilakukan proses 4

54,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53

Kartu setelah dilakukan proses 4

54,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53

Karena kartu terakhir 53 atau 54 maka tidak ada perubahan posisi

Menggunakan cara 2. key masukan dari pengguna

Kartu sebelum dilakukan proses 4

54,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,1(…3)

Kartu setelah dilakukan proses 4

7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53, 54,2,3,4,5,6,1 (…3)

3.3.3 Fase Pengambilan Key

Pada fase ini nilai kartu yang diambil dijadikan masukan untuk membentuk Strean key. Dalam pengambilan key akan dibagi menjadi beberapa cara yang merupakan parameter untuk melakukan optimasi algoritma Pontifex.

Decking kartu yang dijadikan acuan pengambilan key

2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,1(…4)

Cara 1. Pengambilan key sesuai ketentuan dasar algoritma Pontifex

Kartu terkiri adalah 2 sehingga kartu yang diambil menjadi key adalah nilai 4 didapat dengan mencari kartu dengan lokasi 2 ke kanan dari posisi terkiri (kartu bernilai 4).

Cara 2. Pengambilan Key berdasarkan masukan dari prngguna

Melanjutkan dari proses 4 dengan cara key masukan dari user maka key diambil dengan melakukan perhitungan posisi ke kanan sebanyak nilai key yang bersesuaian. Pada contoh di atas digunakan key “FOO” yang berarti perulangan pertama menggunakan karakter F dengan nilai 6. jadi nilai key yang diambil pada proses ini adalah 8 berdasarkan deck (kartu bernilai 6).

3.3.4 Pemisahan Antara Plaintex dan Key

Plaintext dan key dipisahkan dengan melakukan proses balikan dari proses penggabungan.

Proses yang terlibat dalam pemisahan Plaintext dengan Key

• Konversi Ciphertext ke dalam nilai bilangan

• Konversi key ke nilai bilangan

• Kurangkan ke nilai bilangan keduanya

Jika di dapat nilai bilangan negative maka tambahkan nilai 26 atau kelipatannya hingga didapatkan nilai positif kemudian lakukan konversi ke karakter

Proses yang terjadi di definisikan

Tahap 1

Bil_Plaintext =

Konversi_ke_bilangan (Chipertext) – Konversi_ke_bilangan (Key) + (26 * n)

Tahap 2

Plaintext = Konversi_ke_bilangan (Bil_Plaintext)

Dengan n = bilangan integer

Dalam kasus ini nilai n adalah 0,1,2

3.4. Komponen Pendukung

Pemilihan Diffie Hellman dalam pertukaran key dikarenakan metode ini mudah dimengerti tetapi cukup tangguh dalam mengamankan pertukaran data. Jadi tidak kehilangan tujuan dasarnya mengamankan data. Sebagai bahan perbandingan akan dikirimkan key tanpa tanpa menggunakan algoritma pertukaran key. Walaupun akan lebih cepat sebab prosesnya sedikit tetapi sangat tidak aman karena seorang penyadap dapat langsung mengetahui kunci yang kita gunakan.

3.4.1 Pertukaran Key

Pertukaran key yang digunakan adalah menggunakan 3 cara dan merupakan parameter yang menjadi masukan dalam proses implementasi kriptograpi

Cara 1. Key hanya dikirimkan dengan melakukan pengkapsulan dan pengenkapsulsian saja tanpa disandikan . key haruslah dikirim dengan channel yang benar-benar aman. Satu-satunya proteksi pada pengiriman ini adalah dalam keamanan channel. Jika channel disadap maka keseluruhan kunci dapat diketahui.

Cara 2. Ke y dikirimkan dengan menggunakan cara Deffie Hellman

Cara 3. Ke y dikirimkan dengan menggunakan cara Extended Deffie Hellman

3.4.2 Alur Pertukaran Data

Data yang dipertukarkan selain data murni terdapat juga data redudasi yang berfungsi membantu pengiriman data. Data yang perlu dikirimkan sebagai pendukung data terkirim dengan baik adalah

Header Paket

Header ini berupa IP Address, Port asal dan tujuan. Dalam implementasinya terdapat juga header untuk cek error transmisi

Header Data

Header data diberikan pada setiap jenis data yang dikirimkan header data terdiri dari :

• Penanda awal jenis data dikirim

• Penanda akhir jenis data dikirim

• Panjang data

Semua data yang dikirimkan harus memenuhi aturan tersebut agar dijamin keakuratan pengirimannya.

PENUTUP

4.1 Kesimpulan

1. 1. Algoritma kriptograpi pontifex memiliki pembeda dengan algoritma kriptograpi yang lain, yaitu aturan key generator.

   2. Kekuatan Algoritma pontifex relatif sama dengan metode simetris pada umumnya yaitu terletak pada key.

   3. Terdapat empat fase utama pada algoritma kriptograpi pontifex yaitu fase persiapan, fase inti, fase pengambilan key dan fase pemisahan plaintex dengan key.

DAFTAR PUSTAKA

1. Budi Rahardjo (2005), “Keamanan Sistem Informasi Berbasis Internet”, PT Insan Infonesia – Bandung & PT INDOCISC – Jakarta.

1. Stallings, William (1995), “Network and Internetwork Security”, Prentice Hall.

1. Schneier, Bruce (1996), “Applied Cryptography”, Second Edition, John Wiley & Sons.

1. Tanemboum, Andrea S (1996), ”Computer Network”, Prentice Hall.

1. Whitfield Diffie, and Martin E. Hellman, “New Directions in Cryptography,” IEEE Transactions on Information Theory, IT-22, 6, 1976, pp.644-654.

.

ALGORITMA TEA (Tiny Encryption Algorithm)

DESKRIPSI ALGORITMA TEA

Tiny Encription Algorithm (TEA) merupakan suatu algoritma sandi yang diciptakan oleh David Wheeler dan Roger Needham dari Computer Loboratory, Cambridge Univercity, England pada bulan November 1994. Algoritma ini merupakan algoritma penyandian block cipher yang dirancang untuk penggunaan memory yang seminimal mungkin dengan kecepatan proses yang maksimal.

Berikut ini diberikan source code TEA dalam bahasa C, dengan k[0]-k[3]. Dan data dalam v[0] dan v[1]

Encode Routine

void encrypt(unsigned long* v, unsigned long* k) {

unsigned long v0=v[0], v1=v[1], sum=0, i; /* set up */

unsigned long delta=0x9e3779b9; /* a key schedule constant */

unsigned long k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key*/

for (i=0; i < 32; i++) { /* basic cycle start */

sum += delta;

v0 += (v1<<4)+k0 ^ v1+sum ^ (v1>>5)+k1;

v1 += (v0<<4)+k2 ^ v0+sum ^ (v0>>5)+k3; /* end cycle*/

}

v[0]=v0; v[1]=v1;

}

Decode Routine

void decrypt(unsigned long* v, unsigned long* k) {

unsigned long v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */

unsigned long delta=0x9e3779b9; /* a key schedule constant */

unsigned long k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */

for(i=0; i<32; i++) { /* basic cycle start */

v1 -= (v0 << 4)+k2 ^ v0+sum ^ (v0 >> 5)+k3;

v0 -= (v1 << 4)+k0 ^ v1+sum ^ (v1 >> 5)+k1;

sum -= delta; /* end cycle */

}

v[0]=v0; v[1]=v1;

}

System penyandian TEA menggunakan proses feistel network dengan menambahkan fungsi matematik berupa penambahan dan pengurangan sebagai operator pembalik selain XOR. Hal ini dimaksudkan untuk menciptakan sifat non linearitas. Pergeseran dua arah (ke kiri dan ke kanan) menyebabkan semua bit kunci dan data bercampur secara berulang ulang.

TEA memproses 64 bit input sekali waktu dan menghasilkan 64 bit output. TEA menyimpan 64 bit input kedalam L₀ dan R₀ masing masing 32 bit. Sedangkan 128 bit kunci disimpan kedalam k[0], k[1], k[2], dan k[3] yang masing masing berisi 32 bit. Diharapkan teknik ini cukup dapat mencegah penggunaan teknik exshautive search secara efektif. Hasil outputnya akan disimpan dalam L₁₆ dan R_16.

Bilangan delta berasal dari golden number, digunakan delta=(√5 -1)2³¹. Suatu ilangan delta ganda yang berbeda digunakan dalam setiap roundnya sehingga tidak ada bit dari perkalian yang tidak berubah secara teratur. Berbeda dengan sruktur feistel yang semula hanya mengoperasikan satu sisi yaitu sisi sebelah kanan dengan sebuah fungsi F, pada algoritma TEA kedua sisi dioperasikan dengan sebuah fungsi yang sama.

Proses diawali dengan input bit teks terang sebanyak 64 bit. Kemudian 64 bit teks terang tersebut dibagi, yaitu dua. Sisi kiri (L₀) sebanyak 32 bit dan sisi kanan (R₀) sebanyak 32 bit. Setiap bagian teks terang akan dioperasikan sendiri-sendiri. R₀ (z) akan digeser kekiri sebanyak empat (4) kali dan ditambahkan dengan kunci k[0]. Sementara itu z ditambah dengan sum (delta) yang merupakan konstanta. Hasil penambahan ini di XOR kan dengan penambahan sebelumnya. Kemudian di XOR kan dengan hasil penambahan antara Z yang digeser kekenan sebanyak lima (5) kali dengan kunci k[1]. Hasil tersebut kemudian ditambahkan dengan L₀ (y) yang akan menjadi R₁.

Sisi sebelah kiri akan mengalami proses yang sama dengan sisi sebelah kanan. L₀ (y) akan digeser kekiri sebanyak empat (4) kali lalu ditambahkan dengan kunci k[2]. Sementara itu , Y ditambah dengan sum (delta). Hasil penambahan ini di XOR kan dengan penambahan sebelumnya. Kemudian di XOR kan dengan hasil penambahan antara Y yang digeser ke kanan sebanyak lima (5) kali dengan unci k[3]. Hasil tersebut kemudian ditambahkan dengan R₀ (Z) yang akan menjadi L₁.

pergeseran (shift)

Blok teks terang pada kedua sisi yang masing masing sebanyak 32 bit akan digeser kekiri sebanyak empat (4) kali dan digeser ke kanan sebanyak lima (5) kali.

Penambahan

Setelah digeser kekiri stsu kekanan, maka Y dan Z yang sedah digeser akan ditambahkan dengan kunci k[0]-k[3]. Sedangkan Y dan Z awal akan ditambahkan dengan sum (delta).

peng-XOR-an

Setelah dioperasikan dengan penambahan pada masingmasing register maka akan dilakukan peng XOR an dengan rumus untuk satu round adalah sebagai berikut :

y = y + (((z<<4)+k[0])^z+sum^((z>>5)+k[1]))

z = z + (((y<<4)+k[2]^y+sum^((y>>5)+k[3]))

dalam hal ini sum=sum+delta.

Hasil penyandian dalam satu cycle satu blok teks terang 64 bit menjadi 64 bit teks sandi adalah dengan menggabungkan y dan z. Untuk penyandian pada cycle berikutnya y dan z ditukar posisinya, sehingga y₁ menjadi z₁ dan z₁ menjadi y₁ terus dilanjutkan proses seperti langkah-langkah diatas sampai dengan 16 cycle (32 round).

1. Key Schedule

Pada algoritma TEA, key schedulenya sangat sederhana. Yaitu kunci k[0] dan k[1] konstan digunakan ntuk round ganjil sedangkan kunci k[2] dan k[3] konstan digunakan untuk round genap.

5. Dekripsi

Dalam proses delripsi dama halnya seperti dapa proses penyandian yang berbasis feistel cipher lainnya. Yaitu pada prinsipnya adalah sama pada saat proses enkripsi. Namun hal yang berbeda adah penggunaan teks sandi sebagai input dan kunci yang digunakan urutannya dibalik. Pada proses dekripsi semua round ganjil menggunakan k[1] terlebih dahulu kemudian k[0], demikian juga dengan semua round genap digunakan k[3] terlebih dahulu kemudian k[2].

Pada rumus enkripsi diketahui :

L₀ = L₀ + f ( R₀ , k[0], k[1], sum )

R₀ = R₀ + f ( L₀, k[2], k[3], sum )

Sehingga untuk proses dekripsi digunakan rumus :

L₀ = L₀ + f ( R₀ , k[1], k[0], sum )

R₀ = R₀ + f ( L₀, k[3], k[2], sum )

Kriptogarfi Modern

Cipher

System kriptografi simetrik terbagi lagi menjadi dua, diantaranya stream cipher dan blok cipher…

Bedanya???

Pada blok cipher teks terang dibagi menjadi blok – blok dengan panjang tertentu dan ditransformasikan menjadi blok teks sandi dengan panjang yang sama dan dengan mempergunakan kunci yang telah disepakati.

Sedangkan yang namanya stream cipher yaitu dilakukan bit per bit atau karakter per karakter per satuan waktu. Kunci yang digunakan dihasilkan oleh pembangkit rangkaian kunci ( key Stream Generator ). Contoh sream cipher diantaranya ; OTP, RC-4, A5/1 yang digunakan pada handphone dll.

Di bawah ini kita bisa lihat struktur dari stream cipher…

kita bisa lihat dari struktur di atas,sebuah kunci adalah inputan untuk pembangkit rangkaian kunci yang akan menghasilkan sebuah stream number sebanyak 8 bit yang acak. Output dari pembangkit disebut key stream, yang dikombinasikan bit per bit per satuan waktu, plainteks pada stream dengan menggunakan operasi exclusive-OR (XOR). Sebagai contoh, 01101100 sebagai byte yang dibangkitkan oleh pembangkit dan 11001100 adalah plainteks selanjutnya, maka hasil cipherteksnya adalah :

1001100 plainteks

1101100 keystream

0100000 cipherteks

kita ketahui bahwa operasi dari XOR adalah jika inputannya sama maka outputnya bernilai 0.

Dan dalam pendeskripsiannya stream cipher juga menggunakan rangkaian kunci yang sama,

0100000 cipherteks

1101100 key stream

1001100 plainteks

dalam menggunakan stream, ada hal – hal yang harus diperhatikan, diantaranya….

penyandian harus mempunyai periode yang besar, sebuah rangkaian kunci pembangkit menggunakan sebuah fungsi yang menghasilkan bit stream yang akan diulang kembali. Penggunaan periode yang panjang akan sangat sulit dilakukan oleh seorang kriptanalis,, berarti sulit dibuka kan?

Nah.. pada dasarnya perhatian yang sama ini juga ada pada sistem Vigenere , kripanalisis akan sangat sulit dilakukan pada penggunaan kunci yang panjang… yang kedua, kunci yang digunakan dari bilangan random tertutup sebisa mungkin. Contohnya, diperkirakan menggunakan bilangan antara 0 dan 1, jika keys stream digunakan sebagai satu byte pada stream, maka ada 256 byte yang mungkin sering muncul. Kriptanalisis akan kesulitan dengan penggunaan key stream yang acak. Dan satu lagi adalah output dari pembangkit rangkaian kunci dikondisikan menjadi kunci input.

Dengan pembangkit rangkaian kunci, stream cipher dapat seaman blok cipher jika dilihat dari perbandingan kunci yang panjang. pada dasarnya, keuntungan stream cipher yaitu stream cipher lebih cepat dan penggunaan code jauh lebih sedikit dari pada blok cipher. Contohnya pada RC-4, yang dapat diimplementasikan hanya dengan code yang sedikit.

Di bawah ini kita bisa melihat perbandingan kecepatan dari penyandian simetrik pada pentium II.

Algoritma Enkripsi Rivest Code 5 (RC-5)

Algoritma Enkripsi Rivest Code 5 (RC-5)

Abstrak :

RC-5 (Rivest Code-5) merupakan enkripsi stream simetrik yang dibuat oleh RSA Data Security, Inc (RSADSI). Metode enkripsi ini pada awalnya dirancang untuk enkripsi yang menggunakan mikroprosesor (perangkat keras), tetapi pada tahap pengembangannya algoritma ini cocok diterapkan dengan menggunakan perangkat keras maupun perangkat lunak. Secara ringkas algoritma ini bekerja dengan penambahan modulus 2w,melakukan EX-OR dan melakukan rotasi x kekiri dengan jumlah y bit. RC-5 memiliki kelebihan dalam menentukan jumlah kata kunci yang digunakan, hal ini berarti akan memilih tingkat keamanan yang digunakan sesuai dengan aplikasinya. Tulisan ini membahas tentang algoritma enkripsi RC-5 yang dikemukakan oleh Ronald L.Rivest dari MIT Laboratory for Computer Science. Metode penulisan dilakukan dengan studi literartur terhadap buku dan bahasan-bahasan di internet yang berhubungan dengan algoritma enkripsi terutama algoritma RC-5.

1. Pendahuluan
Saat ini sistem komputer yang terpasang makin mudah diakses. Sistem time sharing dan akses jarak jauh menyebabkan masalah keamanan menjadi salah satu kelemahan komuniksi data seperti internet. Disamping itu kecendrungan lain saat ini adalah memberikan tanggung-jawab sepenuhnya ke komputer untuk mengelola aktifitas pridadi dan bisnis seperti sistem transfer dana elekronis yang melewatkan uang sebagai aliran bit dan lain sebagainya. Untuk itu diperlukan sistem computer yang memiliki tingkat keamanan yang dapat terjamin, walaupun pada akhirnya akan terjadi trade off antara tingkat keamanan dan kemudahan akses.
Keamanan komputer adalah menjamin data atau informasi tidak dibaca, tidak dimodifikasi oleh orang lain yang tidak diberi otorisasi. Keamanan sistem dibagi menjadi tiga bagian [4] :

1.Keamanan eksternal
Keamanan eksternal berkaitan dengan fasilitas komputer dari penyusup dan bencana seperti kebakaran atau bencana alam.
2.Keamanan interface pamakai
Keamanan interface pemakai yang berkaitan dengan identifikasi pemakai sebelum pemakai diizinkan mengakses data atau program.
3.Keamanan internal
Keamanan internal berkaitan dengan beragam kendali yang dibangun pada perangkat keras dan perangkat lunak yang menjamin operasi yang handal dan tidak terganngu untuk menjaga integritas data.
Sementara itu kebutuhan keamanan sistem komputer dapat dikategorikan menjadi aspek-aspek sebagai berikut [3] :
1. Privacy / Confidentiality
Inti utama aspek privacy atau confidentiality adalah usaha untuk menjaga informasi dari orang yang tidak berhak mengakses. Privacy lebih kearah data-data yang sifatnya privat sedangkan confidentiality biasanya berhubungan dengan data yang diberikan ke pihak lain untuk keperluantertentu (misalnya sebagai bagian dari pendaftaran sebuah servis) dan hanya diperbolehkan untuk keperluan tertentu tersebut.
2. Integrity
Aspek ini menekankan bahwa informasi tidak boleh diubah tanpa seijin pemilik informasi. Adanya virus, trojan horse, atau pemakai lain yang mengubah informasi tanpa ijin merupakan contoh masalah yang harus dihadapi. Sebuah e-mail dapat saja “ditangkap” (intercept) di tengah jalan, diubah isinya (altered, tampered, modified), kemudian diteruskan ke alamat yang dituju. Dengan kata lain, integritas dari informasi sudah tidak terjaga. Penggunaan encryption dan digital signature, misalnya, dapat mengatasi masalah ini.
3.Authentication
Aspek ini berhubungan dengan metoda untuk menyatakan bahwa informasi betul-betul asli, orang yang mengakses atau memberikan informasi adalah betul-betul orang yang dimaksud, atau server yang kita hubungi adalah betul-betul server yang asli.
4. Availability
Aspek availability atau ketersediaan berhubungan dengan ketersediaan informasi ketika dibutuhkan. Sistem informasi yang diserang atau dijebol dapat menghambat atau meniadakan akses ke informasi.
Enkripsi merupakan salah satu cara yang dilakukan untuk mengamankan sistem atau informasi dari hal yang akan menyebabkan aspek-aspek diatas tidak terpenuhi, seperti untuk menjaga integritas data atau informasi. Ada beberapa algoritma enkripsi yang sudah terbuka untuk dipelajari, seperti Data Encryption Standard (DES), RC-4, Two Fish, RC-5 dan lain-lain. Tulisan ini membahas algoritma RC-5 yang dikemukakan oleh Ronald L.Rivest dari MIT Laboratory for Computer Science. Metode penulisan dilakukan dengan studi literatur terhadap buku dan bahasan-bahasan di internet yang berhubungan dengan algoritma enkripsi terutama algoritma RC-5.

2. Tinjauan Pustaka
Bagian ini membahas tinjaun pustaka yang erkaiatan dengan masalah enkripsi. Diharapakan dengan adanya tinjauan pustaka ini akan memudahkan kita dalam memahami masalha enkripsi terutama enkripsi RC-5.
Salah satu mekanisme untuk meningkatkan keamanan adalah dengan menggunakan teknologi enkripsi. Data-data yang kirimkan diubah sedemikian rupa sehingga tidak mudah disadap. Jadi enkripsi adalah proses yang dilakukan untuk mengamankan sebuah pesan (yang disebut plaintext) menjadi pesan yang tersembunyi (disebut ciphertext) adalah enkripsi (encryption). Ciphertext adalah pesan yang sudah tidak dapat dibaca dengan mudah. Menurut ISO 7498-2, terminologi yang lebih tepat digunakan adalah “encipher”. Proses sebaliknya, untuk mengubah ciphertext menjadi plaintext, disebut dekripsi (decryption). Menurut ISO 7498-2, terminologi yang lebih tepat untuk proses ini adalah “decipher” [3].
Berdasarkan cara memproses teks (plaintext), cipher dapat dikategorikan menjadi dua jenis: block cipher and stream cipher[3]. Block cipher bekerja dengan memproses data secara blok, dimana beberapa karakter / data digabungkan menjadi satu blok. Setiap proses satu blok menghasilkan keluaran satu blok juga. Sementara itu stream cipher bekerja memproses masukan (karakter atau data) secara terus menerus dan menghasilkan data pada saat yang bersamaan.
Banyak servis di Internet yang masih menggunakan “plain text” untuk authentication, seperti penggunaan pasangan userid dan password. Informasi ini dapat dilihat dengan mudah oleh program penyadap atau pengendus (sniffer) [3].
Contoh servis yang menggunakan plaintext antara lain [3]:
• akses jarak jauh dengan menggunakan telnet dan rlogin
• transfer file dengan menggunakan FTP
• akses email melalui POP3 dan IMAP4
• pengiriman email melalui SMTP
• akses web melalui HTTP
Kelompok enkripsi
Kelompok enkripsi itu sendiri dibagi menjadi 3 kelompok yaitu :
1.Symmetric encryption
Menggunakan kunci (key) yang sama untuk proses enkripsi dan dekripsi, masalah yang muncul adalah kesulitan dalam manajemen key. Misalnya dilakukan pengirim data yang telah di enkripsi ke seorang penerima melalui email, orang yang diberi data ini hanya dapat merubah data kedalam bentuk aslinya dengan menggunakan key yang sama. Jadi sipengirim harus memberitahukan ke sipenerima data key key yang digunakan, disini masalahnya bagaimana mengirim key ke penerima tersebut. Bentuk blok diagram metode simetrik diperlihatkan pada gambar 1.

Gambar 1. Enkripsi simetrik
Algoritma enkripsi yang menggunakan metode ini adalah :
Data Encryption Standard (DES)
AES, CAST, IDE, RC-4, RC-5
2.Asymmetric encryption
Menggunakan kunci (key) yang berbeda untuk proses enkripsi dan dekripsi. Pada sistem asimetrik dikenal adanya private key dan public key. Jika melakukan pengiriman data yang di enkripsi ke penerima, sipengrim melakukan enkripsi dengan menggunakan public key dari sipenerima dan data hanya dapat dirobah kembali dalam bentuk plaintext dengan menggunakan private key yang dimiliki sipenerima. Bentuk blok diagram metode asimetrik diperlihatkan pada gambar 2.

Gambar 2. Enkripsi asimetrik
Algoritma enkripsi yang menggunakan metode ini adalah :
RSA
Dife-Hillman
3.Hybrid encryption
Metode ini menggabungkan konsep simetri dan asimetrik, dengan menggunakan key random data dienkripsi dengan metode simetrik. Tahap berikutnya key random yang dipakai untuk proses enkripsi data juga dienkripsi, tetapi menggunakan metode asimetrik dengan menggunakan public key dari sipenerima. Ciphertext yang dihasilkan masing-masing metode digabungkan dan dikirimkan ke penerima. Sipenerima akan membuka Ciphertext untuk key word dengan menggunakan private key yang dimilikinya. Bentuk blok diagram metode ini diperlihatkan pada gambar 3.

Gambar 3.a Proses enkripsi

Gambar 3.b Proses enkripsi
Fungsi Hash Satu Arah

Fungsi hash satu arah (one-way hash function) digunakan untuk membuktikan keaslian dari suatu dokumen atau pesan. Pesan (yang besarnya dapat bervariasi) yang akan di-hash disebut pre-image, sedangkan outputnya yang memiliki ukuran tetap, disebut hash-value (nilai hash). Untuk mengetahui keaslian pesan ada tiga cara yang dapat dilakukan yaitu dengan menggunkan enkripsi dan dekripsi simetrik enkripasi, enkripasi dengan anti simetrik enkripsi dan dengan menggunakan sistem tanda tangan digital. Contoh algoritma fungsi hash satu arah adalah MD-5 dan SHA. Message Authentication Code (MAC) adalah salah satu variasi dari fungsi hash satu arah, hanya saja selain pre-image, sebuah kunci rahasia juga menjadi input bagi fungsi MAC.
Tanda Tangan Digital
Selama ini, masalah tanda tangan digital (digital signature) masih sering di permasalahkan keabsahannya, hal ini terjadi karena pengertian dan konsep dasarnya belum dipahami. Penandatanganan digital terhadap suatu dokumen adalah sidik jari dari dokumen tersebut beserta timestamp-nya di enkripsi dengan menggunakan kunci privat pihak yang menandatangani. Tanda tangan digital memanfaatkan fungsi hash satu arah untuk menjamin bahwa tanda tangan itu hanya berlaku untuk dokumen yang bersangkutan saja. Keabsahan tanda tangan digital itu dapat diperiksa oleh pihak yang menerima pesan.
Sertifikat Digital
Sertifikat digital adalah kunci publik dan informasi penting mengenai jati diri pemilik kunci publik, seperti misalnya nama, alamat, pekerjaan, jabatan, perusahaan dan bahkan hash dari suatu informasi rahasia yang ditandatangani oleh suatu pihak terpercaya. Sertifikat digital tersebut ditandatangani oleh sebuah pihak yang dipercaya yaitu Certificate Authority (CA).
Secure Socket Layer (SSL)
SSL dapat menjaga kerahasiaan (confidentiality) dari informasi yang dikirim karena menggunakan teknologi enkripsi yang maju dan dapat di-update jika ada teknologi baru yang lebih bagus. Dengan penggunaan sertifikat digital, SSL menyediakan otentikasi yang transparan antara client dengan server. SSL menggunakan algoritma RSA untuk membuat tanda tangan digital (digital signature) dan amplop digital (digital envelope). Selain itu, untuk melakukan enkripsi dan dekripsi data setelah koneksi dilakukan, SSL menggunakan RC-4 sebagai algoritma standar untuk enkripsi kunci simetri. Saat aplikasi menggunakan SSL, sebenarnya terjadi dua kondisi, yakni handshake dan pertukaran informasi.
Konsep Dasar RC-5
Seperti dijelaskan diatas, algoritma RC-5 merupakan metode enkripsi menggunakan metode simetrik dan pengolahan dalam bentuk blok chiper, jadi kata kunci yang sama digunakan untuk proses enkripsi dan dekripsi. Parameter-parameter yang digunakan dalam RC-5 adalah sebagai berikut :
Jumlah putaran ini disimbolkan dengan r yang merupakan parameter untuk rotasi dengan nilai 0, 1, 2, …… 255.
Jumlah word dalam bit disimbolkan dengan w. Nilai bit yang di support adalah 16 bit, 32 bit, dan 64 bit.
Kata kunci (key word) Variable ini disimbolkan dengan b dengan range 0, 1, 2, …. 255. Key word ini dikembangkan menjadi array S yang digunakan sebagai key pada proses untuk enkripsi dan dekripsi.
Untuk memahami cara kerja RC-5, dapat dimulai dengan melihat konsep dasar bagaimana RC-5 ini bekerja. Hal ini dilakukan untuk memahami cara kerja algoritma ini lebih lanjut. RC-5 Menggunakan operasi dasar untuk proses enkripsi sebagai berikut :
1.Data yang akan dienkripsi dikembangkan menjadi 2 bagian bagian kiri dan bagian kanan dan dilakukan penjumlahan dengan key word yang yang telah diekspansi sebelumnya. Pemjulahan ditunjukan dengan tanda “+“, dan disimpan di dua register A dan register B.
2.Kemudian dilakukan operasi EX-OR, yang ditandai dengan tanda ““.
3.Melakukan rotasi kekiri (shift left) sepanjang y terhadap x word yang ditandai dengan x<<< y. y merupakan interpretasi modulo w atau jumlah kata w dibagi 2. Dengan lg[w] ditentukan jumlah putaran yang dilakukan.
4.Tahap akhir dilakukan penggabungan untuk mendapatkan data yang telah dienkripsi.
Prose dekripsi dilakukan dengan konsep dasar sebagai berikut :
1.Data yang telah dienkripsi dikembangkan kembali menjadi 2 bagian dan disimpan di dua register A dan register B.
2.Kemudian dilakukan rotasi ke kanan sejumlah r .
3.Selanjutnya dilakukan operasi EX-OR yang ditandai dengan ““.
4.Tahap akhir dilakukan pengurangan terhadap masing-masing register dengan key word yang ditunjukan dengan tanda “-“, untuk mendapatkan plaintext.

3. Algoritma RC-5
Pada bagian ini kita menjelaskan algoritma RC5, yang terdiri dari tiga komponen: algoritma key expansion, algoritma enkripsi, dan algoritma dekripsi.
Input plaintext ke RC5 terdiri dari dua word w-bit, yang ditandai dengan A dan B. RC5 menggunakan expanded key table (key table yang diperluas), S[0…t – 1], terdiri dari t = 2(r + 1) word w-bit. Algoritma key expansion menginisialisasi S dari parameter key rahasia dari (yang diberikan oleh) user. (Sebagai catatan tabel S dalam enkripsi RC5 bukan “S-box” seperti yang yang digunakan di DES; RC5 menggunakan entry dalam S secara sekuensial, satu pada satu waktu).
Diasumsikan konvensi standard “little-endian“ untuk mem-packing byte menjadi blok input/output: byte yang pertama menempati posisi bit low order pada register A, dan seterusnya, sehingga byte keempat menempati posisi bit high-order, byte kelima menempati posisi bit low-order pada B, dan byte kedelapan (terakhir) menempati posisi bit high order di B.
Proses enkripsi
Kita asumsikan bahwa blok input diberikan dalam dua register w-bit A dan B. Kita juga mengasumsikan bahwa key expansion telah dijalankan, sehingga array S[0…t – 1] telah dihitung. Berikut ini adalah algoritma enkripsi dalam pseudo-code.
A=A+S[0];
B=B+S[1];
for i=1 to r do
A=((A  B) <<< B) + S[2 * i];
B=((B A) <<< A) + S[2 * I + 1];
Outputnya berada di dalam register A dan B. Kita mencatat (atau memperhatikan) exceptional simplity dari 5 baris algoritma ini.
Kita juga mencatat bahwa setiap round (putaran) RC5 meng-update kedua register A dan B, dimana satu “round” dalam DES hanya meng-update setengah dari registernya. Suatu “half-round” RC5 (satu dari pernyataan penugasan meng-update A atau B dalam body dari loop diatas) mungkin lebih dapat dianalogi terhadap satu round DES).

Gambar 3. Algoritma enkripsi RC-5
Dari flow chart diatas, A merupakan plaintext yang diproses disebelah kiri setelah ditambahkan dengan dengan hasil key ekspansi dan B merupakan bagian plaintext yang diproses disebelah kanan yang juga ditambahkan dengan hasil key ekspansi. Tahap berikutnya dilakukan proses EX-OR terhadap masing-masing plantext dan dilakukan rotasi (putaran). Setelah dilakukan putaran sebanyak r kali, data-data ini digabungkan kembali membentuk ciphertext yang telah siap dikirimkan ke penerima atau diproses selanjutnya.
Proses dekripsi
Proses dekripsi dilakukan penerima terhadap data yang sudah dalam bentuk ciphertext. Proses ini dapat dilakukan dengan algoritma sebagai berikut :
for i= r downto 1 do
B=((B – S [2 * i + 1]) >>> A)  A;
A=((A – S [2 * i]) >>> B)  B;
B= B- S[1];
A= A – S[0];
Data-data dari ciphertext dikembangkan menjadi dua bagian A dan B selanjutnya di lakukan pengurangan dengan hasil key ekspansi dan dirotasi sebanyak r sambil dilakukan operasi EX-OR terhadap data tersebut. Tahap akhir untuk mendapatkan plaintext adalah dengan melakukan kembali proses pengurangan ke masing-masing bagian dengan hasil key ekspansi. Data-data ini kemudian digabungkan kembali membentuk plaintext sesuai dengan yang dikirimkan pengirim atau data awal sebelum proses enkripsi.
Key Expansion
Rutin key expansion memperluas kunci rahasia user K untuk mengisi array key yang diperluas S, sehingga S menyerupai suatu array t = 2(r + 1) word biner random yang ditentukan oleh K. Algoritma key expansion menggunakan dua “magic constants”, dan terdiri dari tiga bagian algoritmik sederhana.
Definisi dari Magic Constants. Algoritma key-expansion menggunakan dua konstanta biner berukuran word Pw dan Qw. Konstanta biner tersebut didefinisikan untuk sembarang w sebagai berikut :

Dimana :
e = 2.718281828459  Nilai logaritma dasar
 = 1.6180333988749  golden ratio
Dimana Odd(x) (bilangan ganjil (x))adalah integer ganjil (odd) terdekat terhadap x (dibulatkan keatas jika x adalah integer genap, meskipun hal ini tidak terjadi disini). Untuk w = 16, 32, dan 64, konstanta ini diberikan berikut ini dalam biner dan dalam heksadesimal.
P16= 1011011111100001 = b7e1.
Q16= 1001111000110111= 9e37.
P32= 10110111111000010101000101100011 = b7e15163.
Q32=10011110001101110111100110111001 = 9e3779b9.
P62= 1011011111100001010100010110001010001010111011010010101001101011
= b7e151628aed2a6b.
Q64= 1001111000110111011110011011100101111111010010100111110000010101
= 9e3779b97f4a7c15.

Merubah Kunci Dari Bit Ke Word
Langkah algoritmik pertama dari key expansion adalah untuk meng-copy kunci rahasia K[0…b – 1] ke array L[0…e – 1] dari word c = [b/u], dimana u = w/8 adalah jumlah byte/word. Operasi ini dilakukan dalam cara yang alami, menggunakan kunci byte konsekutif (berulang) u dari K untuk memenuhi setiap word dalam L, byte low order sampai byte high order. Posisi byte yang tidak terisi dari L dibuat 0. pada kasus ini b = c = 0 kita me-reset c ke 1 dan me-set L[0] menjadi 0.
Pada mesin “little-endian” seperti pada Intel 486, task diatas dapat diselesaikan hanya dengan membuat array L menjadi 0, dan kemudian meng-copy string K secara langsung ke posisi memori yang merepresentasikan L. Pseudocode berikut ini mencapai efek yang sama, diasumsikan semua byte adalah “unsigned” dan semula array L dibuat 0.
C=[max(b,1)/u]
for i=b-1 downto 0 do
L[i/u]=(L[i/u] <<<8) +K[i];
Menginisialisasi Array S
Langkah algoritmik kedua dari key expansion adalah untuk menginisialisasi array S menjadi pola bit pseudo-random tertentu yang tetap (key-independent), menggunakan deret aritmetika modulo 2w ditentukan oleh “magic constant” Pw dan Qw. Karena Qw ganjil, deret aritmetik memiliki periode 2w.
S[0] = Pw;
for i=1 to t-1 do
S[i] = S[i-1]+Qw;
Dari algoritma diatas terlihat bahwa pada kondisi 0 S[0] berisi Pw dan pada itersi i=1 dan seterusnya, S[i] akan berisi S[i-1] + Qw.
Penggabungan Kunci
Langkah algoritmik ketiga dari key expansion adalah untuk menggabungkan kunci rahasia user dalam tiga cara pada array S dan L. Lebih tepatnya, dikarenakan ukuran yang berbeda secara potensial pada S dan L, array yang lebih besar akan diproses tiga kali, dan yang lainnya dapat ditangani lebih dari tiga kali. Bentuk algoritma proses dapat dilihat berikut ini :
i=j=0;
A=B=0;
do 3 * max(t,c) times
A=S[i]=(S[i]+A+B) << 3;
B=L[j]=(L[j]+A+B) << (A+B);
i=(i+1) mod (t);
j=(j+1) mod(c);

Bentuk Implementasi Dalam Bahasa C
Implementasi ini dilakukan terhadap format RC-5 32bit, 12 putaran dengan 16 byte kata kunci [7].
# include <stdio.h>
typedef unsigned long int WORD; /* Panjang word 32bit=4 byte*/
#define w 32 /* Ukuran word dalam bit*/
#define r 12 /* Jumlah putaran*/
#define b 16 /* Jumlah kata kunci*/
#define c 4 /* Jumlah word*/

#define t 26 /* Ukuran tabel S=2*(r+1)*/

WORD S[t]; /* Tabel pengembangan key*/
WORD P = 0xb7e15163, Q=0x9e3779b9; /* Konstanta magic*/

/* Operasi putaran*/
#define ROTL (x,y) (((x)<<(y&(w-1)))|((x)>>(w-(y&(w-1)))))
#define ROTR (x,y) (((x)>>(y&(w-1)))|((x)<<(w-(y&(w-1)))))

void RC5_ENCRYPT (WORD *pt, WORD *ct) /* proses enkripsi*/
{
WORD i, A=pt[0]+S[0], B=pt[1]+S[1];
for (i=1;i<=r;i++)
{
A=ROTL (A^B,B)+S[2*i];
B=ROTL (B^A,A)+S[2*i+1];
}
ct[0]=A; ct[1]=B;
}

void RC5_DECRYPT (WORD *ct, WORD *pt) /* Proses dekripsi*/
{
WORD i, B=ct[1], A=ct[0];
for (i=r;i>0;i–)
{
B=ROTR (B-S[2*i+1],A)^A;
A=ROTR (A-S[2*i],B)^B;
}
pt[1]=B-S[1]; pt[0]=A-S[0];
}
void RC5_SETUP (unsigned char *k) /* Proses input kunci rahasia*/
{
WORD i, j,k, u=w/8, A, B, L[c];
for (i=b-1,L[c-1]=0;i!=-1;i–)
L[i/u]= (L[i/u]<<8) +K[i];
for (S[0]=P,i=1; i<t; i++)
S[i] = S[i-1]+Q;
for (A=B=i=j=k=0;k<3*t;k++,i=(i+1)%t,j=(j+1)%c)
{
A=S[i]=ROTL (S[i]+(A+B),3);
B=L[j]=ROTL (L[j]+(A+B),(A+B));
}
}
void printword(WORD A) /* Proses input plaintext acak*/
{
WORD k;
for (k=0;k<w;k+=8)
printf (“%02.21X”,(A>>k)&0xFF);
}
void main()/* Program utama*/
{
WORD i,j,k,pt1[2],pt2[2],ct[2]={0,0};
unsigned char key[b];
if (sizeof(WORD) !=4)
printf (“RC5 ERROR : WORD has %d bytes.\n”,sizeof(WORD));
printf (“RC5-32/12/16 examples : \n”);
for (i=1;i<6;i++)
{
pt1[0]=ct[0];pt[1]=ct[1];
for (j=0;j<b;j++)key[j]=ct[0]%(255-j);
RC5_SETUP(key);
RC5_ENCRYPT (pt1,ct);
RC5_DECRYPT(ct,pt2);
printf(“\n%d. key= “,i);
for (j=0;j<b;j++)
printf (“02.2X”,key[j]);
printf (“\n Plaintext “);
printword(pt1[0]);
printword(pt1[1]);
printf(“—-> ciphertext “);
printf word(ct[0]);
print word(ct[1]);
printf(“\n”);
if (pt1[0] !=pt2[0] || pt1[1] !=pt2[1])
printf (“Decryption Error”);
}
}

Hasil simulasi program adalah :
Key = 91 5F 46 19 BE 41 B2 51 63 55 A5 01 10 A9 CE 91
Plaintext = 21A5DBEE154B8F6D
chipertext = F7C013AC5B2B8952

4. Analisis Tingkat Keamanan RC-5
Suatu putaran mengandung dua persamaan yang disimpan dalam buffer A dan B atau dalam bentuk lain. Pada setengah putaran, dapat dijelaskan dengan mengacu kepada persamaan yang dikemukakan oleh Feistel ciphers sebagai berikut;
L1=L0 +S0
R1=R0+S1
For i = 2 to n do
Li= Ri-1
Ri=((Li-1  Ri-1) << Ri-1)+Si
Dari persamaan diatas L1 dan R1 bagian dari plaintext yang dikembangkan menjadi dua bagian kiri dan kanan yang merupakan input dan Li dan Ri adalah merupakan output chipertext. Pada setengah putaran pertama input blok RC-5 (plaintext) adalah L0, R0 dan blok output chipertext adalah Ln, Rn.
Konsep dasar untuk menganalisa cara memecahkan RC-5 dilakukan dengan dengan meganalisa struktur rutin enkripsi, dimana konsep ini berusaha menemukan kunci rahasia dan tabel pengembangan key S. Proses iterasi yang dilakukan untuk mendapatkan kunci rahasia dan tabel pengembangannya didekati dengan perhitungan Ln-1 (b) pada range 0≤ b≤w-1. Pada setengah putaran yang terakhir, Ln dan Rn akan didapat dengan persamaan berikut ini :
Ln = Rn-1;
Rn = (( Ln-1 Rn-1) <<< Rn-1)+Sn
Terdapat 4 variable dalam persamaan kedua diantaranya Rn dan Rn-1, hal ini dapat diketahui dari chipertext. Jika kita mengetahui informasi tentang Ln-1 akan membantu bagaimana mengetahui subkey Sn yang digunakan untuk proses chipertext. Untuk mendapatkan hubungan persamaan dari keempat variable diatas terhadap proses rotasi Rn-1 mod w. Pertama, kita asumsikan kasus khusus dimana (b+Rn-1) mod w = 0. Pada kasus ini bit Ln-1[b])  Rn-1 [b] pindah keposisi bot 0 setelah rotasi. Dengan demikian didapat persamaannya sebagai berikut :
Rn[0]=(Ln-1[b]  Rn-1[b] Sn[0].
Pada awalnya, Rn[0] dan Rn-1[b] diketahui, jika kita dapat menghitung Ln-1[b], selanjutnya dapat diperoleh Sn[0], bit yang kurang penting dari subkey Sn.
Kekuatan dari penyandian bergantung kepada jumlah kunci yang digunakan [3]. Beberapa algoritma enkripsi memiliki kelemahan pada kunci yang digunakan. Untuk itu, kunci yang lemah tersebut tidak boleh digunakan. Selain itu, panjangnya kunci, yang biasanya dalam ukuran bit, juga menentukan kekuatan dari enkripsi. Kunci yang lebih panjang biasanya lebih aman dari kunci yang pendek. Jadi enkripsi dengan menggunakan kunci 128-bit lebih sukar dipecahkan dengan algoritma enkripsi yang sama tetapi dengan kunci 56-bit. Semakin panjang sebuah kunci, semakin besar keyspace yang harus dijalani untuk mencari kunci dengan cara brute force attack atau coba-coba karena keys pace yang harus dilihat merupakan pangkat dari bilangan 2. Jadi kunci 128-bit memiliki keyspace 2128, sedangkan kunci 56-bit memiliki key space 256. Artinya semakin lama kunci baru bisa ketahuan.
Beberapa cara telah dikembangkan oleh seorang pemecah enkripsi untuk menganalisa keamanan block cipher dalam memecahkan chipertext. Jika sebuah key memiliki n bit,kemudian terdapat 2n kemungkinan key yang akan diuji. Ketika ukuran key lebih besar dari ukuran blok, akan terdapat peningkatan kemungkinan pemecahan enkripsi. Test statisktik bisa digunakan untuk menganalisa prilakuk blok chipertext. Blok chipertext yang memiliki tingkat keamanan yang tinggi akan berprilaku seperti suatu permutasi yang random (acak) dari sebuah key yang random juga. Jadi dari informasi dengan statistik diatas sangat sulit untuk memecahkan sebuah enkripsi dengan key dan permutasi yang acak, kecuali dengan analis yang sangat mendalam.
RC-5 menggunakan konsep seperti yang diuraikan diatas, yaitu memiliki jumlah key yang dapat divariasikan dan jumlah rotasi yang dapat ditentukan untuk mendapatkan tingkat keamanan yang diinginkan. Disamping itu proses pengembangan key (key expansion) dilakukan secara acak, yang akan menghasilkan key hasil pengembangan yang juga acak, key hasil pengembangan inilah yang akan digabungkan dengan plaintext. Jadi secara statistik sangat sulit memecahkan kode enkripsi RC-5 yang menggunakan jumlah key yang semakin banyak walapun banyak pihak yang sudah berusaha memecahkan algoritma ini.
Pada tahun 1995 Kaliski dan Yin [7] berhasil memecahkan RC-5 hanya satu tahun setelah dipublikasikan. Mereka melakukan pemecahan dengan menanalisa struktur dasar rutin, yaitu rotasi data idependent, Pada tahun 96` Knudsen dan Meier melakukan perbaikan pemecahan yang dilakukan oleh Kaliski dan Yin dengan menganalisa secara hati-hati hubungan antara input dan subkey. Kemudian pada tahun 1998 Biryukov dan Kushilevitz melakukan perbaikan konsep pemecahan yang dikemukakan oleh Knudsen dan Meier. Mereka mempelajari lebih komplek dan melakukan suatu perkiraan yang umum rotasi data dependent dari enkripsi dan pemecahannya. Mereka memperkirakan untuk memecahkan RC-5 dengan 12 putaran dengan data 64 bit dibutuhkan waktu penyelesaian 255 dan dibuatnya dalam bentuk tabel berikut ini untuk data 64 bit:
Jumlah Putaran
4
6
8
10
12
14
16
18
Iterasi proses plaintext
(chosen plaintext)
27
216
228
236
244
252
261
>
Iterasi pemecahan plaintext
(known plaintext)
236
241
247
251
255
259
263
>

Dari uraian dan tabel diatas dapat disimpulkan, bahwa RC-5 dapat dipecahkan dan membutuhkan waktu iterasi pemecahan yang cukup lama tergantung jumlah putaran yang digunakan seperti yang terlihat pada tabel diatas berdasarkan syarat dibaris kedua dan ketiga. Semakin tinggi jumlah putaran yang dilakukan semakin lama proses pemecahan, dimana jumlah putaran ditentukan saat prose enkripsi. Jumlah putaran juga menentukan tabel pengambangan key yang digunakan. Jadi semakin banyak jumlah kata kunci dan putaran yang digunakan, maka semakin lama waktu yang dibutuhkan untuk memecahkan enkripsinya dan tingkat keamanan semakin tinggi.

5. Feature-Feature RC-5
Algoritma memiliki keuntungan-keuntungan dalam implementasinya. Hal ini dapat digunakan oleh pemakai untuk memilih atau sebagai pertimbangan dalam memilih menggunakan RC-5 [5].
Keuntungan-keuntungan yang dimiliki RC-5 adalah sebagai berikut:
RC-5 menggunakan metode enkripsi simetrik, sehingga key yang sama digunakan untuk proses enkripsi dan dekripsi.
RC-5 dapat diimplentasikan dengan hard ware ataupun soft ware, dimana RC-5 menggunakan dasar operasi komputasi yang biasa digunakan pada konsep dasar mikroprosesor.
RC-5 mempunyai kemampuan proses enkripsi dan dekripsi yang cepat, besar nya kemampuan ini diperlihatkan dengan cara kerja beroreantasi pada kata (word).
RC-5 dapat disesuaikan untuk bermacam-macam prosesor yang memiliki panjang bit data yang berbeda. Contohnya untuk prosesor 64 bit dapat dipakai untuk RC-5 dengan panjang kata yang diolah lebih panjang atau disesuaikan dengan kemampuan prosesor tersebut.
RC-5 memiliki struktur yang iterative dengan variabel jumlah rotasi (putaran), sehingga pengguna secara eksplisit dapat memanipulasi trade off antara kecepatan dan tingkat keamanan.
RC-5 mempunyai variabel panjang key word yang dapat divariasikan, sehingga pengguna dapat memilih tingkat keamanan yang dikehendaki sesuai dengan aplikasi yang digunakan.
RC-5 sangat sedehana sehingga mudah untuk diimplementasikan.
RC-5 membutuhkan memori yang kecil.

6. Pengembangan RC-5
Pengembangan RC-5 didasari kepada keinginan untuk mendapatkan tingkat keamanan yang tinggi agar sulit dipecahkan. Ada beberapa pengembangan yang sudah dilakukan diantaranya [7]:
A. RC5XOR
Konsep pengembangan ini didasari kepada proses pertukaran penjumlahan dengan operasi EX-OR. Jadi semua operasi dasar penjumlahan digantikan dengan operasi EX-OR seperti pada algoritma berikut ini :
Ri=((Li-1 Ri-1) <<< Ri-1)  Si
B. RC5P
Konsep pengembangan ini berlawanan dengan proses diatas, yaitu dengan melakukan pertukaran operasi EX-OR dengan operasi penjumlahan. Jadi operasi yang dilakukan terhadap plaintext hanya dilakukan operasi penjumlahan.
Ri=((Li-1+ Ri-1) <<< Ri-1) + Si
C. RC5PFR
Konsep pengembangan ini memasukan jumlah putaran ri dengan jumlah yang tetap. Proses putaran diberikan dengan nilai yang tetap dan tidak tergantung pada pengembangan sisi kanan dari plaintext.
Ri=((Li-1 Ri-1) <<< ri) + Si
D. RC5KFR
Konsep pengembangan ini memasukan jumlah putaran ri (K) yang didapat dari kunci rahasia K. Konsep putaran yang digunakan tergantung kepada jumlah key yang digunakan. Jadi semakin banyak jumlah key yang digunakan semakin banyak jumlah putaran yang dilakukan.
Ri=((Li-1 Ri-1) <<< ri(K)) + Si
F. RC5RA
Konsep pengembangan ini memasukan jumlah putaran f (Ri-1) yang teragnatung pada jumlah bit Ri-1.
Ri=((Li-1 Ri-1) <<< f(Ri-1)) + Si
G. RC6
Pengembangan yang terbaru dari RC-5 disebut dengan RC-6. Konsep dasar pengembangan ini menggunakan putaran fungsi kuadratik berikut ini terhadap 5 bit bagian atas. f(x)=x(2x+1) mod 223.

7. Penutup
Pada kondisi nyata, semua algoritma enkripsi data yang ada masih dapat dipecahkan kuncinya oleh para kritoanalis, hal ini menunjukan bahwa tidak ada algoritma enkripsi data yang sempurna, termasuk juga disini algoritma RC-5. Untuk enkripsi model RC-5 masih terdapat beberapa kelebiha dan kelemahan yaitu diantaranya;.
A.Kelebihan
Kesulitan mengetahui sebuah nilai dalam table pengembangan key karena prose pengembangan key dilakukan secara random.
Algoritma enkripsi ini dapat diimplementasikan dalam bentuk hard ware, karena pada dasarnya algoritm in menggunakan operasi yang dapat dilakukan oleh perangkat keras seperti prosesor. Hal ini telah dibuktikan oleh E. Chitalwala1, T. El-Ghazawi1, N.Alexandridis1 dan K.Gaj2.
1 The George Washington University, Washington DC.
2 George Mason University, Fairfax.

Tingkat keamanan dari enkripsi yang dilakukan dapat dipilih dengan
menggunakan jumlah kata kunci yang digunakan, hal ini terlihat bahwa jumlah kata kunci akan menentukan jumlah pembagian plaintext yang akan dienkripsi.
B.Kekurangan
Algoritma RC-5 dapat diserang dengan menggunakan analisa dari bagian table pengembangan kunci rahasia.
Salah satu kelemahan umum dari metode enkripsi simetrik adalah masalah manajemen kunci. Hal ini juga terdapat pada RC-5, dimana penerima harus memiliki kunci yang sama untuk membuka chipertext yang dikirimkan kepadanya. Hal ini juga merupakan suatu kelemahan yang dapat dimanfaatkan oleh penyerang.
Daftar Pustaka
1.Bruce Schneier, Applied Cryptography : Protocols, Algorithms, and Source Code in C, 2nd Edition
2.Wahana Komputer & Andi Yogyakarta,” Penanganan Jaringan Komputer”, Semarang, Yogyakarta,2002.
3.Budi Rahardjo,” Keamanan Sistem informasi Berbasis Internet”, PT Insan Komunikasi Indonesia, Bandung, 2002.
4.Bambang Hariyanto,”Sistem Operasi”,Jilid I, Informatika Bandung,1997.
5.Kristianto, Andi, KEAMANAN DATA pada JARINGAN KOMPUTER, Gava Media, Yogyakarta, 2003
6.Wahana Komputer Semarang, Memahami MODEL ENKRIPSI & SECURITY DATA, Andi Offset, Yogyakarta, 2003
7.http://grc.com/r&d/rc5-report.pdf
8.ftp://ftp.auscert.org.au/pub/coast/COAST/Tripwire/*

SCOP ” THE FAST STREAM CIPHER “

SCOP “THE FAST STREAM CIPHER”

 

A.Abstraksi

SCOP merupakan salah satu contoh dari kriptografi kunci simetrik, dalam hal ini stream cipher. SCOP diciptakan oleh Simeon V. Maltchev dan Peter T. Antonov, kemudian dikembangkan secara khusus, sehingga terciptalah SCOP yang lebih efisien kinerjanya pada prosesor Intel Pentium. Secara teoritis SCOP dapat mengerjakan 1,5 clock cycles per byte. Skema cipher ini didisain dengan sebuah S-box yang key dependent, dengan bagian pertama berubah secara dinamis pada proses enkripsi dan sebagian lagi merupakan bagian statik. Cipher ini bekerja dalam internal-feedback mode (IFB). Keystream terdiri dari 32-bit word dan dihasilkan secara independen dari pesan enkripsi. Algoritma enkripsi SCOP tidak dipatenkan oleh penciptanya, sehingga source codenya dapat digunakan oleh siapa saja dengan acara mendownloadnya lewat internet, tanpa harus membayarkan royalti kepada penciptanya.

B.Pendahuluan

Kriptografi, secara umum adalah ilmu dan seni untuk menjaga kerahasiaan berita [bruce Schneier – Applied Cryptography]. Selain pengertian tersebut terdapat pula pengertian ilmu yang mempelajari teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan data, keabsahan data, integritas data, serta autentikasi data [A. Menezes, P. van Oorschot and S. Vanstone – Handbook of Applied Cryptography]. Namun tidak semua aspek keamanan informasi ditangani dengan menggunakan teori-teori kriptografi.Pada dasarnya terdapat 4(empat) tujuan mendasar dari ilmu kriptografi. Hal tersebut juga merupakan bagian dari aspek-aspek keamanan informasi yaitu :

• Kerahasiaan, adalah layanan yang digunakan untuk menjaga isi dari informasi dari siapapun kecuali yang memiliki otoritas atau kunci rahasia untuk membuka/mengupas informasi yang telah disandi.

• Integritas Data, adalah berhubungan dengan penjagaan dari perubahan data secara tidak sah. Untuk menjaga integritas data, sistem harus memiliki kemampuan untuk mendeteksi manipulasi data oleh pihak-pihak yang tidak berhak, antara lain penyisipan, penghapusan, dan pensubsitusian data lain kedalam data yang sebenarnya.

• Autentikasi, adalah berhubungan dengan identifikasi/pengenalan, baik secara kesatuan sistem maupun informasi itu sendiri. Dua pihak yang saling berkomunikasi harus saling memperkenalkan diri. Informasi yang dikirimkan melalui kanal harus diautentikasi keaslian, isi datanya, waktu pengiriman, dan lain-lain.

• Non-repudiasi, atau penyangkalan adalah usaha untuk mencegah terjadinya penyangkalan terhadap pengiriman/terciptanya suatu informasi oleh yang mengirimkan/membuat.

Dalam kriptografi terdapat 2(dua) proses utama yaitu menyandi(enkripsi) dan membuka sandi(dekripsi). Proses menyandi/enkripsi dapat diartikan juga sebagai kode atau cipher. Sebuah sistem pengkodean menggunakan suatu tabel atau kamus yang telah didefinisikan untuk kata dari informasi atau yang merupakan bagian dari pesan, data, atau informasi yang akan dikirimkan. Sebuah cipher menggunakan suatu algoritma yang dapat mengkodekan semua aliran data(stream) yang berbentuk bit dari suatu pesan asli(plaintext) menjadi sebuah cryptogram yang tidak dapat dimengerti, kecuali jika dibuka/didekripsikan kembali menjadi plaintext.

Pengamanan pesan, data, atau informasi tersebut selain bertujuan untuk meningkatkan keamanan, juga berfungsi untuk:

• Melindungi pesan, data, atau informasi agar tidak dapat di baca oleh orang-orang yang tidak berhak.

• Mencegah agar orang-orang yang tidak berhak, menyisipkan atau menghapus pesan, data, atau informasi.

Sistem kriptografi sendiri terbagi menjadi tiga macam, yaitu sistem kriptografi kunci simetrik, sistem kriptografi kunci publik(asimetrik), dan sistem kriptogafi fungsi hash. Sistem kriptografi kunci simetrik merupakan sistem kriptografi yang menggunakan satu macam kunci dalam melakukan proses enkripsi dan dekripsi. Pada sistem ini keamanan dalam proses transmisi dan berita tergantung pada tingkat kerahasiaan kunci dan kompleksitasan algoritma yang digunakan. Kunci memegang peranan yang sangat penting sehingga harus dirahasiakan dan diamankan oleh penggunanya. Karena kunci yang digunakan harus dirahasikan dan diamankan, maka kunci yang digunakan pada sistem kriptografi kunci simetrik, biasanya disebut dengan sebutan kunci rahasia(secret key).

Skema kriptografi kunci simetrik yang didasarkan kepada jumlah data perproses dan alur pengolahan data didalamnya dapat dibedakan menjadi dua kelas, yaitu block-cipher dan stream-cipher. Block-cipher adalah skema algoritma sandi yang akan memilah-milah teks terang yang akan dikirimkan dengan ukuran tertentu (disebut juga dengan blok) dengan panjang t, dan setiap blok dienkripsi dengan menggunakan kunci yang sama. Pada umumnya, block-cipher memproses teks terang dengan blok yang relatif panjang lebih dari 64 bit, hal ini dilakukan untuk mempersulit penggunaan pola-pola serangan yang ada dalam usaha pembongkaran kunci. Selain itu untuk menambah ketangguhan model algoritma block cipher, dikembangkanlah beberapa tipe proses enkripsi, yaitu(ECB, CBC, OFB dan CFB).

Sedangkan stream-cipher adalah algoritma sandi yang mengenkripsi data persatuan data, seperti bit, byte, nible atau per lima bit(saat data yang akan enkripsi data tersebut berupa data Boudout). Setiap mengenkripsi satu satuan data di gunakan kunci yang merupakan hasil pembangkitan dari kunci sebelum.

C.Deskripsi Algoritma SCOP

Seperti diterangkan pada bagian sebelumnya, SCOP didisain khusus untuk digunakan pada prosesor Intel Pentium, namun penggunaan SCOP tetap dapat berjalan dengan cepat pada prosesor 32-bit lainnya. Selain itu SCOP juga didisain untuk memenuhi kriteria sebagai berikut:

• Bekerja pada mode IFB, keystream dihasilkan secara independen dari pesan enkripsi.

• Kompak, SCOP dapat berjalan pada memori kurang dari 2,5 Kbyte.

• Implementasi software yang simpel, SCOP menggunakan operasi sederhana seperti penambahan dan pengurangan modulus 2³² dan tabel lookup.

• Keamanan variabel, SCOP merupakan algoritma ukuran kunci variabel, dengan ukuran kunci sampai dengan 384 bit.

Algoritma ini mempunyai dua bagian yaitu key expansion dan enkripsi data. Bagian pertama merubah kunci, yang bisa sampai dengan panjang 48 byte menjadi array 1540 bytes. Key expansion ini berdasarkan pada fungsi hash satu arah yang dinamakan GP8. Operasi utama yang digunakan dalam proses cipher adalah penambahan aritmetis dari 32-bit words. Operasi tambahan adalah 4 tabel lookup, yang dilakukan untuk setiap word yang akan dienkripsi.

SCOP menggunakan sebuah 32-bit S-box (dinamai V) dengan 384 entri, dua 8-bit indek i dan j, dan tiga buah variabel sementara T1, T2, T3. S-box dibagi dua: pertama merupakan 128 32-bit word dari V membentuk bagian bagian pertama yang statis, dan kemudian 256 32-bit word dari V membentuk bagian kedua yang berubah-ubah selama proses enkripsi. Indek j menunjuk hanya bagian yang dinamis, sedangkan indek i menunjuk bagian statis dan setengah bagian dinamis.

S-box V diinisialisasi dengan 1536 byte pertama dari expanded key. Tiga byte berikutnya dari epanded key digunakan untuk menginisialisasi indek i dan j, dan variabel sementara T3 (24 high bit dari T3 dinisialisasi dengan 0). Penggunaan sebuah byte terakhir dari expanded key sedikit spesial: hanya 7 bit darinya yang digunakan. Byte ini digunakan sebagai index array dari bagian statis dari S-box V, kemudian isi dari array yang diindek oleh byte spesial ini dibuat ganjil tanpa memperhatikan apakah isinya ganjil atau genap. Keystream K 32-bit dihasilkan dengan langkah-langkah sebagai berikut: 1. T1 = V[128 + j] 2. j = (j + T3) mod 256 3. T2 = V[128 + j] 4. T3 = V[128 + j] + V[i] 5. V[128 + j] = T3 6. i = (i + 1) mod 256 7. j = (j + T2) mod 256 8. K = T1 + T2 K kemudian ditambahkan pada plainteks untuk menghasilkan cipherteks atau dikurangkan dari cipherteks untuk menghasilkan plainteks.

D.Cara Kerja

Main instructions/Instruksi utama dari SCOP dapat dikodekan dengan 15 instruksi assembler pada setiap prosesor 32 bit, yang mempunyai paling tidak 6 buah register dan mempunyai instruksi untuk: memindah data dari memori ke register dan dari register ke memori; penambahan dan pengurangan dua buah register; penambahan register dengan nilai immediate dan pengurangan nilai immediate dari register; mask register dengan nilai immediate (instruksi AND). Bila prosesor mampunyai register (paling tidak 4) yang memberikan akses langsung pada bagian 8 bit, seperti AL untuk EAX, ketiga instruksi mask tidak dibutuhkan dan algoritma dapat dikodekan dengan 12 instruksi. Ke-12 instruksi ini termasuk dua instruksi untuk membaca dan menulis dari/ke plainteks/cipherteks yang sedang diproses dan satu instruksi untuk mengkombinasikan dengan keystream.

Ke-12 instruksi ini secara teoritis dapat dieksekusi dengan 6 clock cycle pada Pentium. Dengan demikian berarti SCOP dapat mengenkrip data pada 1,5 Pentium clock cycle per byte, karena seperti kita ketahui algoritma ini bekerja pada 32-bit word (4 byte) sekaligus. Berdasarkan kinerja pada prosesor Pentium dari SEAL dan RC4 [3], maka SCOP 2,5 kali lebih cepat dari SEAL dan 4,5 kali lebih cepat dari RC4.

E.Implementasi Algoritma SCOP

Implementasi dari algoritma enkripsi data yang merupakan salah satu bagian dari SCOP(fungsi enkripsi/dekripsi) pada aslinya ditulis dalam bahasa Assembler Intel. Namun aplikasi(fungsi enkripsi/dekripsi) yang tertera dibawah ini sudah berupa bahasa berasas menengah, yaitu bahasa C.

/* Demo program SCOP(The Fast Stream Cipher) */
/* SCOP is tested with MSVC 4.1 and 5.0, and with gcc 2.7.x. Please be careful with Borland’s 32-bit C compiler. Read the comment in the encrypt/decrypt functions. */

#include <stdio.h>

#include <assert.h>

#define MESSAGE_WORDS 1024 typedef struct

{

unsigned long v[384];

unsigned char i;

unsigned char j;

unsigned char t3;

}

st_key; typedef struct { unsigned char coef[8][4]; unsigned long x[4];}

st_gp8; st_key kt;st_gp8 int_state;

unsigned long buf[MESSAGE_WORDS];

static void gp8 (unsigned long *out);

static voidexpand_key (unsigned char *in, unsigned in_size)

{ unsigned i; unsigned char *p;

unsigned char counter;

assert (in_size >= 2 && in_size <= 48);

p = (unsigned char *) &int_state;

for (i = 0; i < in_size; i++) p[i] = in[i];

for (i = in_size; i < 48; i++)

p[i] =(unsigned char) (p[i – in_size] + p[i – in_size + 1]);

counter = 1; for (i = 0; i < 32; i++)

{ if (p[i] == 0) p[i] = counter++; }}

voidinit_key (unsigned char *in, unsigned in_size)

{ unsigned long odd; unsigned long t[4]; int i, j; expand_key (in, in_size);

for (i = 0; i < 8; i++)

gp8 (t); for (i = 0; i < 12; i++)

{ for (j = 0; j < 8; j++) gp8 (kt.v + i * 32 + j * 4); gp8 (t); }

gp8 (t); kt.i = (unsigned char) (t[3] >> 24);

kt.j = (unsigned char) (t[3] >> 16);

kt.t3 = (unsigned char) (t[3] >> 8);

odd = t[3] & 0×7f; kt.v[odd] |= 1; }

/* partially optimized version */

static voidgp8 (unsigned long *out)

{ unsigned long y1, y2, x_1, x_2, x_3, x_4;

unsigned long newx[4]; int i, i2;

for (i = 0; i < 8; i += 2) { i2 = i >> 1;

x_1 = int_state.x[i2] >> 16; x_2 = x_1 * x_1;

x_3 = x_2 * x_1; x_4 = x_3 * x_1;

y1 = int_state.coef[i][0] * x_4 + int_state.coef[i][1] * x_3 + int_state.coef[i][2] * x_2 + int_state.coef[i][3] * x_1 + 1; x_1 = int_state.x[i2] & 0xffffL;

x_2 = x_1 * x_1; x_3 = x_2 * x_1;

x_4 = x_3 * x_1;voidinit_key (unsigned char *in, unsigned in_size)

{ unsigned long odd; unsigned long t[4]; int i, j; expand_key (in, in_size);

for (i = 0; i < 8; i++) gp8 (t); for (i = 0; i < 12; i++) { for (j = 0; j < 8; j++) gp8 (kt.v + i * 32 + j * 4);

gp8 (t); }

gp8 (t);

kt.i = (unsigned char) (t[3] >> 24);

kt.j = (unsigned char) (t[3] >> 16);

kt.t3 = (unsigned char) (t[3] >> 8);

odd = t[3] & 0×7f; kt.v[odd] |= 1;} y2 = int_state.coef[i + 1][0] * x_4 +

int_state.coef[i + 1][1] * x_3 +

int_state.coef[i + 1][2] * x_2 +

int_state.coef[i + 1][3] * x_1 + 1;

out[i2] = (y1 << 16) | (y2 & 0xffffL);

newx[i2] = (y1 & 0xffff0000L) | (y2 >> 16); }

int_state.x[0] = (newx[0] >> 16) | (newx[3] << 16); int_state.x[1] = (newx[0] << 16) | (newx[1] >> 16); int_state.x[2] = (newx[1] << 16) | (newx[2] >> 16);

int_state.x[3] = (newx[2] << 16) | (newx[3] >> 16);}

/* partially optimized version */

voidencrypt (unsigned long *buf, int buflen, st_key *skey)

{ unsigned char i, j; unsigned long t1, t2, t3;

unsigned long k, t; unsigned long *word, *v; i = skey->i; j = skey->j;

t3 = skey->t3; v = skey->v; word = buf; while (word < buf + buflen)

{ t1 = v[128 + j]; j += t3; t = v[i];

t2 = v[128 + j];

/* If you want to compile with Borland’s 32-bit C compiler using

optimizations, change the line below to:

i = (i + 1) & 255; */

i++;

t3 = t2 + t;

v[128 + j] = t3;

j += t2;

k = t1 + t2;

*word++ += k; }}

/* partially optimized version */

voiddecrypt (unsigned long *buf, int buflen, st_key *skey)

{ unsigned char i, j; unsigned long t1, t2, t3;

unsigned long k, t;

unsigned long *word, *v; i = skey->i; j = skey->j; t3 = skey->t3; v = skey->v; word = buf;

while (word < buf + buflen)

{

t1 = v[128 + j];

j += t3;

t = v[i];

t2 = v[128 + j];

/* If you want to compile with Borland’s 32-bit C compiler using

optimizations, change the line below to:

i = (i + 1) & 255; */

i++;

t3 = t2 + t;

v[128 + j] = t3;

j += t2;

k = t1 + t2;

voidmain (void){ unsigned char key[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,14, 15};

unsigned long t; int i, flag; printf (”1\n”);

init_key (key, sizeof (key));

printf (”2\n”);

for (i = 0; i < MESSAGE_WORDS; i++) buf[i] = 0L;

printf (”3\n”); encrypt (buf, MESSAGE_WORDS, &kt);

printf (”4\n”);

t = 0L;

for(i = 0; i < MESSAGE_WORDS; i++) t ^= buf[i];

printf (”XOR of buf is %08lx.\n”,t);

init_key (key, sizeof (key));

decrypt (buf, MESSAGE_WORDS, &kt); flag = 0;

for (i = 0; i < MESSAGE_WORDS; i++) { if (buf[i] != 0L) flag = 1; }

if (flag) printf (”Decrypt failed.\n”);

else printf (”Decrypt succeeded.\n”);

}

F.Penutup

Demikianlah isi dari blog saya di awal pagi hari yang selalu cerah akhir-akhir ini, meskipun pusing, harus tetap semangat, ngomong-ngomong tolong BANGET tinggalkan komentar/comment pada blog saya ini karena hal tersebut merupakan suatu penghargaan bagi saya, karena hasil pekerjaan saya telah anda baca dan anda nilai, selain itu hal tersebut juga akan dinilai oleh dosen saya. Semoga isi dari blog ini berguna bagi anda, komunitas, telebih untuk Negara dan Bangsa, amin.

Kata-kata terakhir sebelum saya tutup blog ini mungkin adalah permohonan maaf kepada para pembaca jikalau terdapat kata-kata pada blog ini yang dirasa menyinggung perasaan anda baik yang disengaja maupun yang tidak disengaja, karena kesalahan datangnya dari saya, dan kebenaran datangnya dari Allah S.W.T.

Dan Selamat Hari Raya Idul Fitri 1428 H, bagi yang merayakannya, Minal Aizin Wal Faizin, Mohon maaf Lahir, dan Batin. Sekian Wass. Wr. Wb.

 

HIDUP MAHASISWA…!!!!!

G.Daftar Pustaka

1. http://id.wikipedia.org/wiki/Kriptografi

2. Simeon V. Maltchev and Peter T. Antonov, “The SCOP Stream Cipher” , ftp://ftp.funet.fi/pub/crypt/cryptography/symmetric/scop/scop.tar.gz, Dec. 1997.

3. Agner Fog, “How to optimize for the Pentium family of microprocessors”, http://agner.org/assem/pentopt1.zip, 1999.

4. Bruce Schneier and Doug Whiting,“Fast software encryption: Designing encryption algorithms for optimal software speed on the Intel Pentium processor”, http://www.counterpane.com/fast_software_encryption.pdf, 1977

 

Oleh : Sandromedo C.N.

NPM : 0605100703

Awal dan Arti Kata ” Persandian “

Persandian di Republik Indonesia

Dalam kamus besar bahasa Indonesia kata persandian yang berasal dari kata dasar sandi adalah rahasia atau kode; definisi sinonimnya dalam bahasa Inggris cryptography, yang berarti pengetahuan, studi, atau merupakan seni tentang tulisan yang bersifat rahasia.

Pada era perkembangan teknologi informasi dan komunikasi saat ini, pengertian umum persandian adalah semua kegiatan pengamanan informasi rahasia yang dilaksanakan berdasarkan konsep, teori dari teknik-teknik penyandian (enkripsi), serta ilmu pendukung lain secara metodologis, konsisten, dansistematis.

dr Roebiono Kertopati, Bapak Persandian Indonesia

Persandian Negara Indonesia didirikan pada tanggal 4 April 1946 oleh Mayor Jenderal dr. Roebiono Kertopati. Beliau adalah seorang dokter kepresidenan di masa Presiden RI Pertama Soekarno. Persandian negara Indonesia tersebut sekarang dikenal dengan nama Lembaga Sandi Negara dan dr Roebiono Kertopati sebagai Kepala Lembaga Sandi Negara yang pertama.

Bapak Roebiono Kertopati yang lahir di Ciamis pada tanggal 11 Maret 1914 sebelum dan selama perang dunia II tidak pernah bekerja dalam bidang persandian / kriptografi. Suami dari Amalia Achmad Atmadja ini adalah seorang dokter yang pada waktu itu menjabat sebagai dokter (medis) di Kementerian Pertahanan RI bagian B (intelijen). Karena pada masa itu, tidak seorang pribumipun dipercaya Belanda untuk bekerja dalam bidang persandian.